Comportamiento del Campo Eléctrico en una
nube de tormenta: Relación Townsend - Podestá
Introducción
En el Paper nº2 sobre Electricidad de la Atmósfera bajo
el título "Dependencia del Gradiente de Potencial
Eléctrico de la Atmósfera con la Humedad Relativa y la
Velocidad del Viento" llegamos después de mucho tiempo
de experimentos y mediciones a la ecuación diferencial:
k1 dE + E2 (dh - k2
dv)=0
Ecuación diferencial de E=F(h,v), (Campo Eléctrico E en
función de la Humedad Relativa y de la Velocidad del
Viento).
La solución de esta ecuación diferencial es la ecuación:
E= k1( h-k2 v)-1
Llamada Ecuación de Podestá, en donde esta es parte de
un trabajo de investigación desarrollado para una tesis.
La constantes k1 y k2 son
constantes empíricas encontradas por el Autor cuyos
valores son: 8652.61 v/m.% (volt/metro) y 1.00 % (m/s)-1
respectivamente.
En el caso particular que v=0 entonces la ecuación se
reduce al caso particular:
E0= k1h-1
Lo llamaremos Campo Eléctrico inicial.
Descargas eléctricas a
través de un gas
La descarga Eléctrica a través de un gas que continúa
después de cesar la acción del agente ionizante, se
denomina "Descarga Gaseosa Automantenida".
Las cargas Eléctricas Libres necesarias para mantener la
descarga surgen principalmente como resultado de la
ionización por choques de las moléculas del gas con los
electrones (ionización volumétrica) y el arranque de
electrones del cátodo al bombardearlo con iones
positivos (ionización superficial). La ionización por
choques de las moléculas del gas con los iones positivos
hay que tenerla en cuenta solamente en el caso de Campos
Eléctricos muy intensos. El arranque de electrones del
cátodo puede producirse también al calentarlo (emisión
termo-iónica o termo-electrónica) y debido al efecto
fotoeléctrico exterior relacionado con la luminiscencia
de la descarga (fotoemisión).
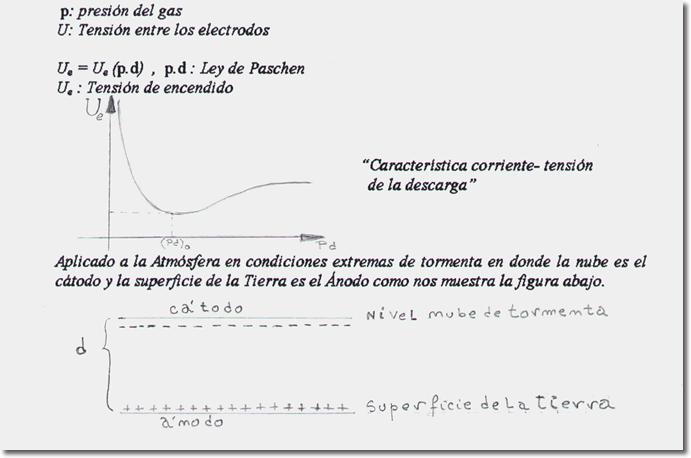
El paso de la descarga no autónoma a través del gas, a
la descarga automantenida de este se denomina descarga
eléctrica disruptiva en el gas y se produce a la tensión
de encendido Ue (tensión de potencial
disruptiva).
? (ead - 1)=1
Condición de TOWNSEND (para que salte una chispa), en
donde:
a: Valor medio de la cantidad de ionización producida
por un electrón en un recorrido de longitud unidad
(coeficiente de ionización volumétrica).
d: Distancia entre los electrodos.
?: Coeficiente de ionización superficial (Es igual al
número de electrones arrancados al cátodo por un ion
positivo).
e: carga eléctrica elemental
Para un gas y material del cátodo dado tenemos:
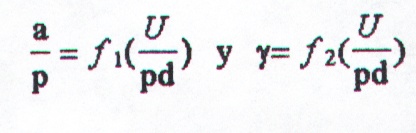
Observemos que ? nunca va a ser cero, por lo tanto
siempre existen electrones arrancados por un ion
positivo. En una tormenta será la superficie de la
Tierra que le quita a la nube. Durante tiempo bueno lo
hace el aire a la tierra; y de esta manera se mantiene
el equilibrio.
Relación Townsend - Podestá
Buscando establecer una relación entre las ecuaciones,
primero se encuentra que:
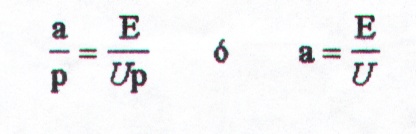
E: Campo Eléctrico
U: Tensión
En estas relaciones existe un factor de proporcionalidad
que permiten la igualdad.
De la Ecuación Podestá:
E= E0 (1-k2 vh-1)-1
donde: ?= (1-k2vh-1)-1
entonces: E= ?E0, V=?V0, ? = ??0
Estas son las "Ecuaciones Básicas de la Electricidad de
la Baja Atmósfera" de PODESTÁ.
Estas las relacionaremos con la Ecuación de TOWNSEND y
de esta manera lograremos las Ecuaciones Básicas en las
condiciones de Campos Eléctricos en una nube de tormenta
en donde los campos eléctricos superan los 1000 v/m
(recordar que el campo eléctrico en tiempo bueno es de
100 v/m).
Tabla comportamiento Campo Eléctrico versus Humedad:
E0=100 v/m
v= 10 m/s v=20 m/s
| h |
E |
h |
E |
| 11 |
1100 |
21 |
2100 |
| 20 |
200 |
30 |
300 |
| 30 |
150 |
40 |
200 |
| 40 |
133,3 |
50 |
166,7 |
| 50 |
125 |
60 |
150 |
| 60 |
120 |
70 |
140 |
| 70 |
116,7 |
80 |
133,3 |
| 80 |
114,3 |
90 |
128,6 |
| 90 |
112,5 |
100 |
125 |
| 100 |
111,1 |
|
|
Asumiremos que:
a=E0 V-1
Si ead = ?-1+1 y aplicando
logaritmo a ambos miembros tenemos:
Ln ead = Ln (? -1+ 1), y
despejando a=(d Ln e)-1 Ln(?-1 +
1)
Entonces la relación nos queda:
E = a ?V0, si multiplicamos numerador y
denominador por ad y operamos convenientemente tenemos:
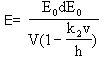
finalmente sabiendo que d/V= 1/E nos queda:
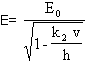
En esta ecuación E0 no puede tener valores
normales, sino mucho más altos que son los que tenemos
en una nube de tormenta.
A la raíz cuadrada del denominador la vamos a llamar
"Factor de Atenuación" del Campo Eléctrico en el caso
particular de una tormenta eléctrica.
Referencias
Theory of Electric Conductivity Measurements by an
Electrostatic Probe in an Atmospheric Low-Density
Continuum Ionized Gas - Chang and Kodera (Paper 5D002 -
Journal of Geophysical Research).
Electricidad de la Atmósfera - Podestá (Paper del Centro
de Estudios de Física Atmosférica C.E.F.A. - Córdoba -
Argentina).
Todos los Derechos Reservados. Nro. de Registro 361 -
Registro Nacional del Derecho de Autor - Paraguay.
|
